그래프 알고리즘 중 Union-Find 에 대해서 공부한 내용입니다.
잘못된 부분이 있을 수 있습니다. 잘못된 부분이 있다면 지적부탁드립니다!
유니온 파인드(Union-Find)란?
여러개의 노드가 존재할 때 두개의 노드를 선택해서, 현재 두 노드가 서로 같은 그래프에 속해있는지 판별하는 알고리즘입니다.
그래프에서 사이클이 존재하는지 여부를 판별할 때 유용하게 사용됩니다.
유니온 파인드(Union-Find) 그림 설명
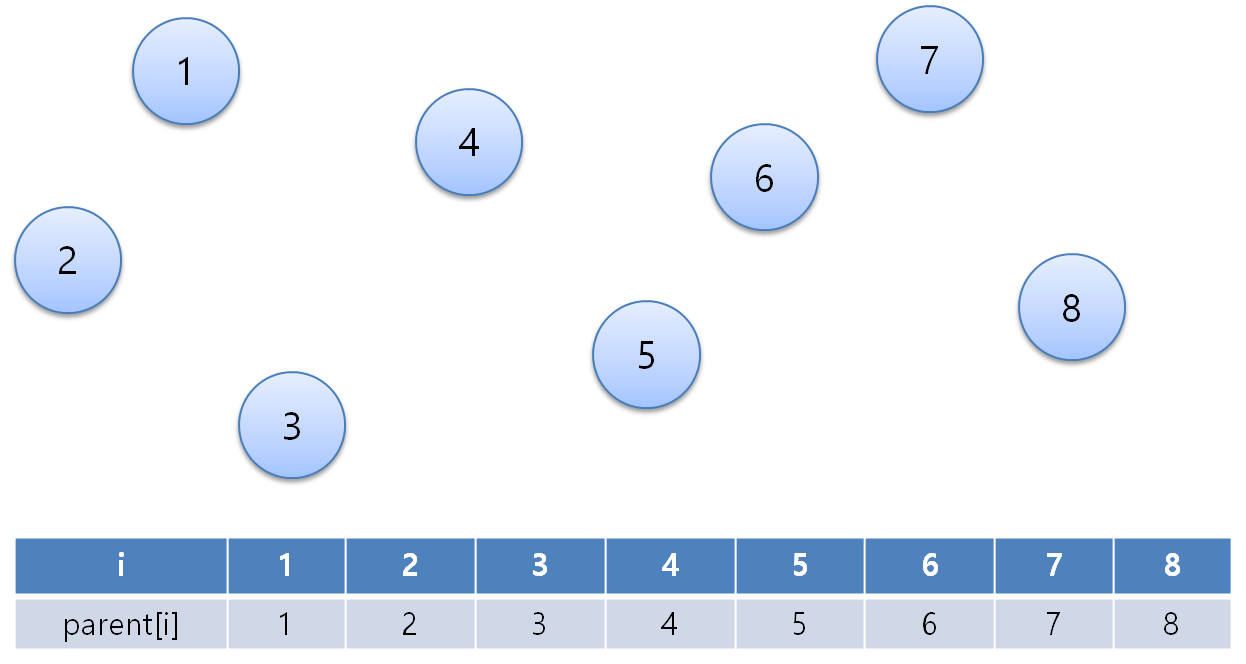
위 그림과 같이 여러개의 노드가 모두 연결되지 않고, 자기 자신만을 집합의 원소로 가질 때 모든 값이 자기 자신을 가르키도록 합니다.
그리고 표를 보면 i는 노드 번호, parent[i]는 부모 노드 번호를 의미합니다. 즉, 자기 자신이 어떤 부모에 포함되어있는지를 의미합니다.
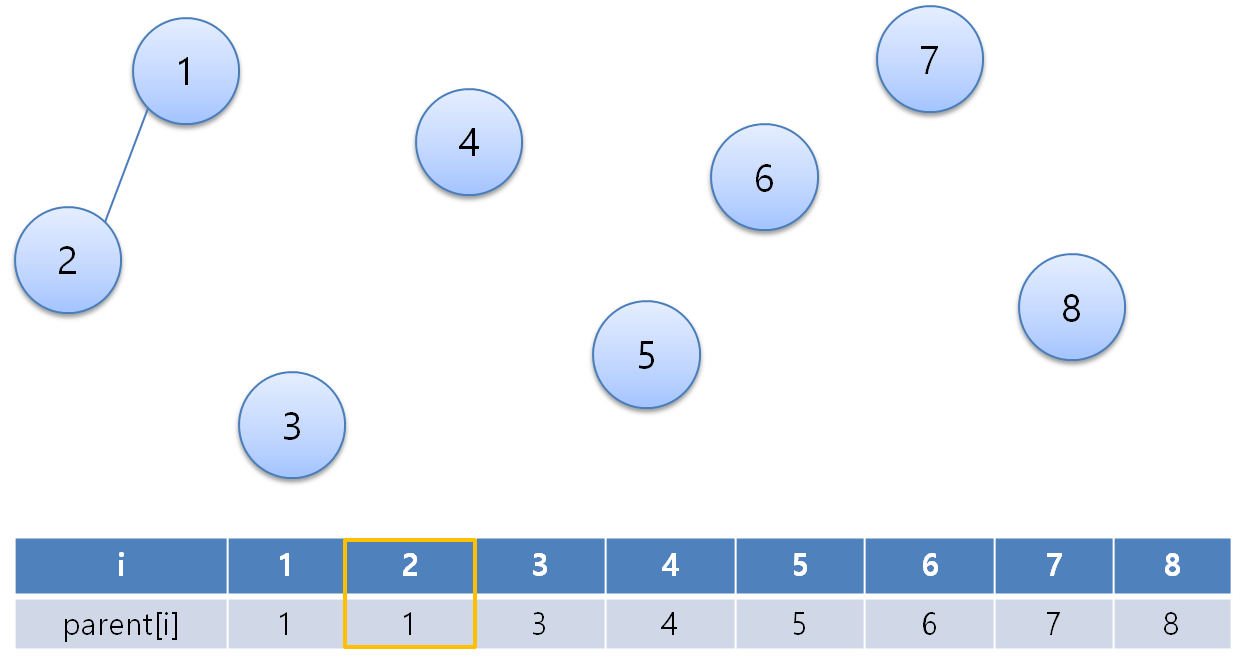
자 이제, 1번 노드와 2번 노드를 연결해보도록 하겠습니다.
1번 노드와 2번 노드를 연결하면 위 표와 같이 표현이 되고, 2번 노드는 1번 노드에 포함되게 됩니다.
일반적으로 부모를 합칠 때 더 작은 값 쪽으로 합칩니다. 이 것을 합침(Union) 과정이라고 합니다.
이번엔 2번 노드와 3번 노드를 연결해보도록 하겠습니다.
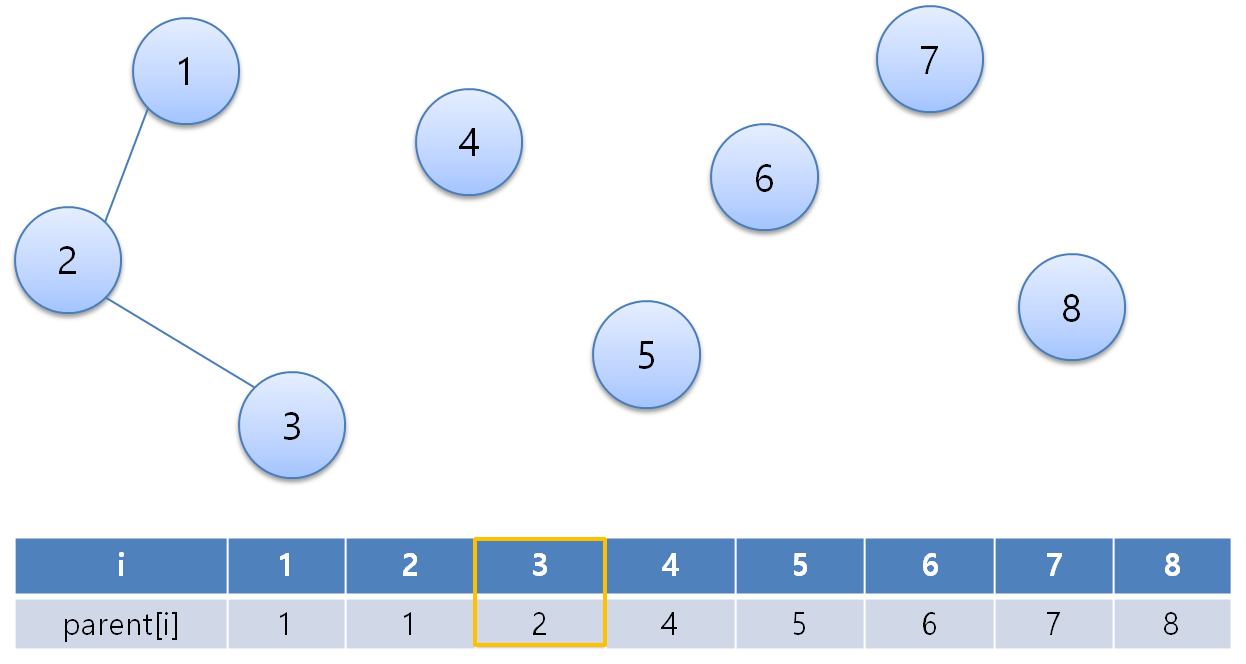
2번 노드와 3번 노드가 연결되면 3번 노드의 부모 노드 번호는 2로 바뀌게 됩니다.
그렇다면 3번 노드는 1번 노드와 연결되었는지 어떻게 알 수 있을까요?
1과 3은 부모 노드 번호가 각 1과 2로 다르기 때문에 부모 노드 번호만 보고 알 수 없습니다.
그래서 여기서 재귀 함수가 사용됩니다.
3의 부모를 찾기 위해 먼저 3의 부모 노드인 2를 찾습니다. 그리고 2의 부모 노드인 1을 찾아 결과적으로 3의 부모 노드는 1이 되는 것을 알 수 있습니다.
그래서 합침(Union)과정이 수행 된 이후에 표는 아래와 같이 변경되게 됩니다.

그래서 1, 2, 3번 노드가 부모가 모두 1로 동일하므로 같은 그래프에 속한다고 할 수 있습니다.
➔ Find : 2개 노드의 부모 노드를 확인하여 같은 그래프에 속하는지 확인하는 알고리즘
유니온 파인드(Union-Find) 구현
유니온 파인드(Union-Find)를 구현하면 아래와 같습니다.(주석 포함)
#include <bits/stdc++.h>
using namespace std;
// 부모 노드 찾기(재귀 함수)
int getParent(vector<int>& parent, int x) {
if(parent[x] == x) return x;
else return parent[x] = getParent(parent, parent[x]);
}
// 두 부모 노드를 합침
void unionParent(vector<int>& parent, int x, int y) {
x = getParent(parent, x);
y = getParent(parent, y);
if(x == y) return; // 부모 노드를 확인했을 때 같다면 이미 연결되어 있음
// 더 작은 값으로 합침
if(x < y) parent[y] = x;
else parent[x] = y;
}
bool findParent(vector<int>& parent, int x, int y) {
// 같은 그래프에 속해있는지?
x = getParent(parent, x);
y = getParent(parent, y);
if(x == y) return true; // 같은 그래프
else return false; // 다른 그래프
}
void printParent(vector<int>& parent) {
// 노드별 부모 노드 확인
int len = parent.size();
for(int i = 1; i < len; ++i) {
cout << parent[i] << ' ';
}
cout << '\n';
}
int main(void) {
vector<int> parent;
for(int i = 0; i <= 8; ++i) {
parent.emplace_back(i); // 실제 노드 번호는 1 ~ 8
}
printParent(parent); // 현재 parent : 1, 2, 3, 4, 5, 6, 7, 8
unionParent(parent, 1, 2); // 1번 노드와 2번 노드 연결
unionParent(parent, 2, 3); // 2번 노드와 3번 노드 연결
unionParent(parent, 4, 5); // 4번 노드와 5번 노드 연결
unionParent(parent, 5, 6); // 5번 노드와 6번 노드 연결
// 1번 노드와 4번 노드는 연결되어 있는가?
if(findParent(parent, 1, 4) == false) {
// 연결되어있지 않음 -> 출력
cout << "Disconnect" << '\n';
} else {
// 연결됨
cout << "Connect" << '\n';
}
unionParent(parent, 1, 4); // 1번 노드와 4번 노드 연결
// 1번 노드와 4번 노드는 연결되어 있는가?
if(findParent(parent, 1, 4) == false) {
// 연결되어있지 않음
cout << "Disconnect" << '\n';
} else {
// 연결됨 -> 출력
cout << "Connect" << '\n';
}
return 0;
}'Algorithm' 카테고리의 다른 글
| [Algorithm] 크루스칼(Kruskal) (0) | 2022.09.05 |
|---|---|
| [Algorithm] 이분 탐색(Binary Search) (0) | 2022.08.31 |
| [Algorithm] 다익스트라(Dijkstra) (0) | 2022.08.23 |
| [Algorithm] 최장 증가 부분 수열(LIS) (0) | 2022.08.17 |
| [Algorithm] 에라토스테네스의 체 (0) | 2022.08.02 |


댓글